траєкторія руху

1. Визначення та основні поняття траєкторії руху У багатьох задачах інтерес представлю не тільки переміщення...
2. оборотність руху
3. Параметри траєкторії руху
4. Приклади завдань з рішенням

Визначення та основні поняття траєкторії руху

У багатьох задачах інтерес представлю не тільки переміщення матеріальних точок в просторі, але і траєкторії їх руху.

визначення

Лінію, яку описує частка при своєму русі, називається траєкторією руху.

Залежно від форми траєкторії механічний рух можна розділити на:

• прямолінійний рух, траєкторією руху точки в цьому випадку є пряма лінія;
• і криволінійне переміщення (траєкторія - крива лінія).

Форма траєкторії залежить від вибору системи відліку. У різних системах відліку траєкторії можуть бути представлені різними лініями, можуть бути прямими і кривими.

При русі точки з постійним прискоренням, яке описує рівняння:

\ [\ Overline {r} \ left (t \ right) = {\ overline {r}} _ 0 + {\ overline {v}} _ 0t + \ frac {\ overline {a} t ^ 2} {2} \ left (1 \ right), \]

(Де $ \ overline {r} \ left (t \ right) $ - радіус-вектор точки в момент часу $ t $; $ {\ overline {v}} _ 0 $ - початкова швидкість руху точки; $ \ overline {a} $ - прискорення точки,) траєкторія руху являє собою плоску криву, що означає всі крапки цієї кривої знаходяться в одній площині. Положення цієї площини в просторі задають вектори прискорення і початкової швидкості. Орієнтацію координатних осей найчастіше вибирають так, щоб площина руху збігалася з однієї з координатних площин. В цьому випадку векторна рівняння (1) можна звести до двох скалярним рівнянням.

Рівняння траєкторії руху

Розглянемо вільний рух тіла біля поверхні Землі. Початок координат розмістимо в точці кидання тіла (рис.1). Осі координат спрямуємо так, як зображено на мал.1.

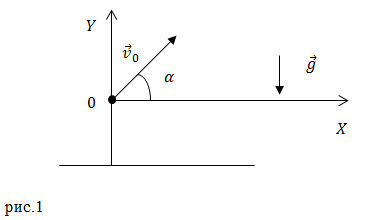
Тоді рівняння руху тіла (1) в проекціях на координатні осі декартової системи координат набуває вигляду системи з двох рівнянь:

\ [\ Left \ {\ begin {array} {c} x = v_0t {\ cos \ alpha \ left (2 \ right), \} \\ y = v_0t {\ sin \ alpha \} - \ frac {gt ^ 2} {2} \ left (3 \ right). \ End {array} \ right. \]

Для того щоб отримати рівняння траєкторії руху тіла ($ y = y (x) $) слід виключити час руху тіла з рівнянь (2) і (3). Висловимо з рівняння (2) $ t $ і підставимо його в вираз (3), отримаємо:

\ [T = \ frac {x} {v_0 {\ cos \ alpha \}}; \ y = v_0 \ frac {x} {v_0 {cos \ alpha \}} {\ sin \ alpha \} - \ frac {g } {2} {\ left (\ frac {x} {v_0 {cos \ alpha \}} \ right)} ^ 2 \ to y = x \ tg \ \ alpha - \ frac {gx ^ 2} {2v ^ 2_0 {cos} ^ 2 \ alpha} \ left (4 \ right). \]

Вираз (4) це рівняння параболи, що проходить через початок координат. Її верві спрямовані вниз, так як коефіцієнт при $ x ^ 2 $ менше нуля.

Вершина цієї параболи знаходиться в точці з координатами:

\ [\ Left \ {\ begin {array} {c} x = \ frac {v ^ 2_0 {\ sin \ alpha {\ cos \ alpha \} \}} {g} \\ y = \ frac {v ^ 2_0 {sin} ^ 2 \ alpha} {2g} \ end {array} \ right. \ left (5 \ right). \]

Знайти координати вершини траєкторії можна за допомогою відомих правил дослідження функцій на екстремум. Так, положення максимуму функції $ y (x) $ визначають, прирівнюючи до нуля першу похідну ($ \ frac {dy} {dx} $) від неї по $ x $.

оборотність руху

З уявлення про траєкторії можна конкретизувати зміст оборотності механічного руху.

Нехай частинка рухається в силовому полі такому, що її прискорення в будь-якій точці має певну величиною, що не залежить від швидкості. Як буде рухатися ця частка, якщо, в якій точці її траєкторії напрямок швидкості замінити протилежним? З точки зору математики це еквівалентно заміні $ t \ $ на $ -t $ для всіх рівнянь. Рівняння траєкторії час не містить, виходить, що частка буде переміщатися «назад» по тій же самій траєкторії. При цьому відрізки часу між будь-якими точками траєкторії будуть однакові при прямому і зворотному русі. Будь-якої точки траєкторії ставиться у відповідність певне значення величини швидкості незалежно від напрямку руху по даній траєкторії. Дані властивості наочні в коливальних рухах маятника.

Все сказане вище справедливо тоді, коли можна знехтувати будь-яким опором руху. Оборотність руху існує, коли виконується закон збереження механічної енергії.

Параметри траєкторії руху

Положення точок системи відліку можна визначати за допомогою різних способів. Відповідно до цих способами описують і рух точки або тіла:

• Координатна форма опису руху. Вибирається система координат, в ній положення точки характеризують трьома координатами (в тривимірному просторі). Це можуть бути координати $ x_1 = x, x_2 = y, x_3 = z $, в декартовій системі координат. $ X_1 = \ rho, x_2 = \ varphi, x_3 = \ z $ в циліндричній системі і т.д. При переміщенні точки координати є функціями часу. Описати рух точки - це означає вказати ці функції:
\ [X_1 = x_1 \ left (t \ right) ;; \ x_2 = x_2 \ left (t \ right) ;; \ x_3 = x_3 \ left (t \ right) \ left (6 \ right). \]
• При описі руху в векторній формі положення матеріальної точки задає радіус-вектор ($ \ overline {r} $) по відношенню до точки, яку приймають за початкову. У цьому випадку вводять точку (тіло) відліку. При переміщенні точки вектор $ \ overline {r} $ постійно змінюється. Кінець цього вектора описує траєкторію. Рух задає вираз:
\ [\ Overline {r} = \ overline {r} \ left (t \ right) \ left (7 \ right). \]
• Третім способом опису руху є опис за допомогою параметрів траєкторії.

Шлях - це скалярна величина, що дорівнює довжині траєкторії.

Якщо траєкторія задана, то завдання опису руху зводять до визначення закону руху уздовж неї. При цьому вибирається початкова точка траєкторії. Будь-яка інша точка характеризується відстанню $ s $ по траєкторії від початкової точки. В такому випадку рух описують виразом:

\ [S = s \ left (t \ right) \ left (8 \ right). \]

Нехай по колу радіуса R рівномірно переміщається точка. Закон руху точки по колу в розглянутому методі запишемо як:

\ [S = At ​​\ left (9 \ right), \]

де $ s $ - шлях точки по траєкторії; $ T $ - час руху; $ A $ - коефіцієнт пропорційності. Відомими є окружність і точка початку руху. Відлік позитивних величин $ s $ збігається з напрямком переміщення точки по траєкторії.

Знання траєкторії руху тіла в багатьох випадках істотно спрощує процес опису руху тіла.

Приклади завдань з рішенням

приклад 1

Завдання: Точка рухається в площині XOY з початку координат зі швидкістю $ \ overline {v} = A \ overline {i} + Bx \ overline {j} \, \ $ де $ \ overline {i} $, $ \ overline {j } $ - орти осей X і Y; $ A $, B - постійні величини. Запишіть рівняння траєкторії руху точки ($ y (x) $). Зобразіть траєкторію. \ Textit {}

Рішення: Розглянемо рівняння зміни швидкості частинки:

\ [\ Overline {v} = A \ overline {i} + Bx \ overline {j} \ \ left (1.1 \ right). \]

З цього рівняння випливає, що:

\ [\ Left \ {\ begin {array} {c} v_x = A, \\ v_y = Bx \ end {array} \ right. \ Left (1.2 \ right). \]

З (1.2) маємо:

\ [Dx = v_xdt = Adt \ to dt = \ frac {dx} {A} ;; dy = v_ydt = Bxdt \ to dy = Bx \ frac {dx} {A} \ \ left (1.3 \ right). \]

Для отримання рівняння траєкторії слід вирішити диференціальне рівняння (1.3):

\ [Y = \ int \ limits ^ x_0 {\ frac {B} {A}} xdx = \ frac {B} {2A} x ^ 2. \]

Ми отримали рівняння параболи, гілки якої спрямовані вгору. Ця парабола проходить через початок координат. Мінімум цієї функції знаходиться в точці з координатами:

\ [\ Left \ {\ begin {array} {c} x = 0 \\ y = 0. \ End {array} \ right. \]

приклад 2

Завдання: Рух матеріальної точки в площині описує система рівнянь: $ \ left \ {\ begin {array} {c} x = At. \\ y = At ​​(1 + Bt) \ end {array} \ right. $, Де $ A $ і $ B $ - позитивні постійні. Запишіть рівняння траєкторії точки.

Рішення: Розглянемо систему рівнянь, яка задана в умові завдання:

\ [\ Left \ {\ begin {array} {c} x = At. \\ y = At ​​\ left (1 + Bt \ right) \ end {array} \ right. \ Left (2.1 \ right). \]

Виключимо час з рівнянь системи. Для цього з першого рівняння системи висловимо час, отримаємо:

\ [T = \ frac {x} {A} \ left (2.2 \ right). \]

Підставами замість $ t $ праву (2.2) частина в друге рівняння системи (2.1), маємо:

\ [Y = At ​​\ left (1 + Bt \ right) = At ​​+ ABt ^ 2 = A \ frac {x} {A} + AB {(\ frac {x} {A})} ^ 2 = x + \ frac {B} {A} x ^ 2. \]

Відповідь: $ y = x + \ frac {B} {A} x ^ 2 $

Читати далі: прискорення тіла .