Підбір апроксимуючої кривої для експериментальних даних в COMSOL Multiphysics

1. Підбір кривої як завдання мінімізації функції
2. Рішення завдання в COMSOL
3. подальші розширення
4. висновок

Ми часто обробляємо в COMSOL Multiphysics експериментальні дані. Зазвичай вони характеризують властивості матеріалів або інші вхідні параметри моделі. Однак експериментальні дані часто бувають зашумленими; вони містять похибки експерименту, які ми не хотіли б вносити в модель. У цій статті ми розповімо, як підбирати гладкі криві і поверхні під експериментальні дані, використовуючи базові функціональні можливості COMSOL Multiphysics.

Підбір кривої як завдання мінімізації функції

Давайте подивимося на графік з експериментальними точками, представлений нижче. Ми бачимо, що дані зашумлені, а вибірка по осі x нерівномірна. Ці експериментальні дані можуть характеризувати матеріал. Якщо характеристика матеріалу залежить від змінної, розраховувати в ході рішення, (наприклад, теплопровідність, що залежить від температури), то ці початкові дані зазвичай не бажано безпосередньо використовувати для кінцево-елементного аналізу. Такі зашумлені вхідні дані часто можуть викликати проблеми зі збіжністю решателя з причин, розглянутим тут . Якщо ж ми аппроксимируем дані гладкою кривою, то збіжність моделі, як правило, покращується, а характеристика матеріалу буде представлена ​​більш простою функцією.

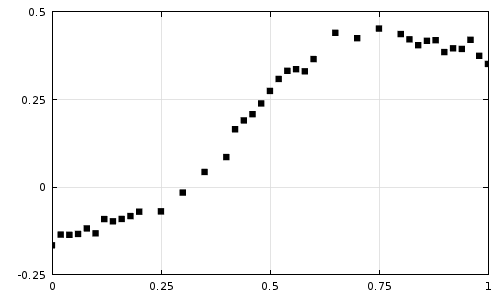
Експериментальні дані, які ми хочемо апроксимувати простою функцією.

Нам потрібно знайти функцію F (x), яка є найбільш точним наближенням експериментальних даних D (x). "Найбільш точне значення" тут означає функцію, що мінімізувала інтеграл квадрата різниці експериментальних даних і значень нашої наближеною функції, взятий по всьому набору даних. Іншими словами, ми хочемо мінімізувати

\ Int_a ^ b (D (x) - F (x)) ^ 2 dx

В першу чергу ми повинні вирішити, яким класом функцій ми хочемо апроксимувати дані. Ми можемо вибирати різні класи функцій, при цьому обрана апроксимуюча функція повинна досить просто обчислюватися. Опускаючи докладний обгрунтування, для максимальної стійкості виберемо таку функцію:

F (x) = c_0 \ left (\ frac {bx} {ba} \ right) ^ 3 + c_1 \ left (\ frac {xa} {ba} \ right) \ left (\ frac {bx} {ba} \ right) ^ 2 + c_2 \ left (\ frac {xa} {ba} \ right) ^ 2 \ left (\ frac {bx} {ba} \ right) + c_3 \ left (\ frac {xa} {ba} \ right) ^ 3

В окремому випадку, коли a = 0, а b = 1, вона має спрощений вигляд:

F (x) = c_0 (1-x) ^ 3 + c_1 x (1-x) ^ 2 + c_2 x ^ 2 (1-x) + c_3 x ^ 3

Тепер потрібно знайти чотири коефіцієнта, що забезпечують мінімальне значення виразу:

R (c_0, c_1, c_2, c_3, x) = \ int_a ^ b (D (x) - F (c_0, c_1, c_2, c_3, x)) ^ 2 dx

Це схоже на задачу оптимізації, але ми не вводимо обмежень на коефіцієнти і припускаємо, що функція має єдиний мінімум. У точці цього мінімуму похідні функції за коефіцієнтами дорівнюватимуть нулю. Тому для підбору найкращої функції ми повинні знайти такі значення коефіцієнтів, що

\ Frac {\ partial R} {\ partial c_0} = \ frac {\ partial R} {\ partial c_1} = \ frac {\ partial R} {\ partial c_2} = \ frac {\ partial R} {\ partial c_3 } = 0

Виявляється, це завдання можна вирішити за допомогою базових функцій COMSOL Multiphysics. Давайте подивимося, як це зробити.

Рішення завдання в COMSOL

Ми починаємо зі створення нового файлу з одновимірним компонентом. Ми скористаємося інтерфейсом фізики Global ODEs and DAEs (Глобальні звичайні диференціальні рівняння і алгебраїчні диференціальні рівняння), щоб знайти шукані коефіцієнти, і будемо використовувати стаціонарний вирішувач. Для простоти виберемо безрозмірну одиницю довжини, як показано на знімку екрана нижче.

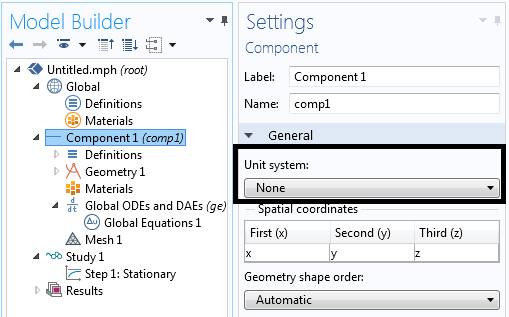
В налаштуваннях вузла 1D component (Одновимірна компонент) в поле Unit system (Система одиниць) виберіть None (Безрозмірна).

Далі задамо геометрію. Геометрія задачі складається з інтервалу (експериментальні точки в нашому випадку лежать в інтервалі від 0 до 1) і безлічі точок по осі x для кожної експериментальної точки. Ви можете просто скопіювати цей набір точок з електронної таблиці і вставити в поле Point (Точка), як показано нижче.

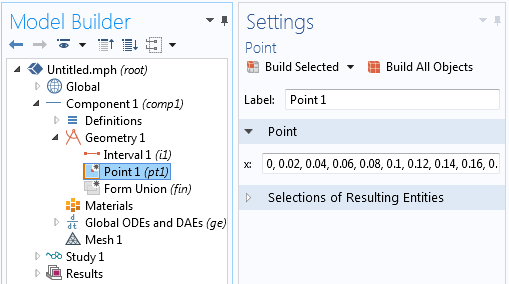
Додайте точки, відповідні експериментальним даними, в інтервал.

Вважайте експериментальні дані за допомогою функції Interpolation (Інтерполяція). Дайте набору даних зручне ім'я (на знімку екрана внизу використано просто D), активуйте опцію Use spatial coordinates as arguments (Використовувати просторові координати в якості аргументів) і переконайтеся, що обраний варіант інтерполяції між точками даних за замовчуванням - Linear (Лінійна).

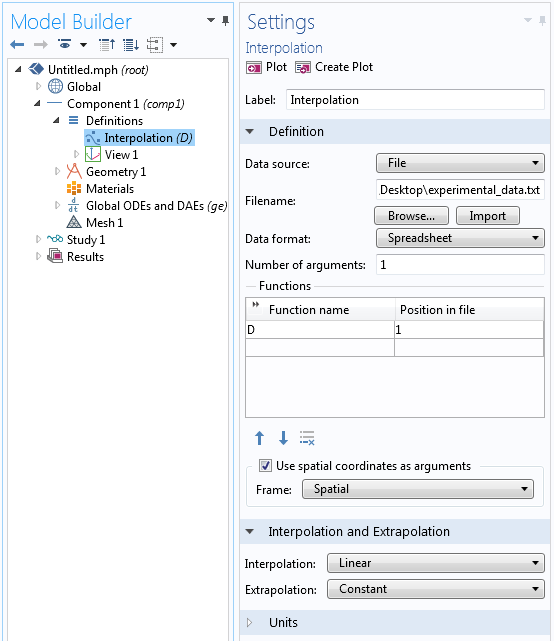
Налаштування імпорту експериментальних даних.

Задайте оператор інтегрування (Integration) на всіх областях. Ви можете залишити найменування за замовчуванням, intop1. Він буде використовуватися для обчислення зазначеного вище інтеграла.

Оператор інтегрування заданий на всіх областях.

Тепер задайте дві змінних. Одна з них буде вашої функцією F, а інша - функцією R, яку потрібно мінімізувати. Так як в поле Geometric Entity Level (Рівень геометричних об'єктів) обраний варіант Entire Model (Вся модель), функція F буде задана на всій області як функція просторової змінної x. З іншого боку, R всюди задана скалярним значенням і також доступна по всій моделі. Як показано на знімку екрана нижче, ми можемо ввести F як функцію c_0, c_1, c_2, c_3, а самі коефіцієнти визначимо пізніше.

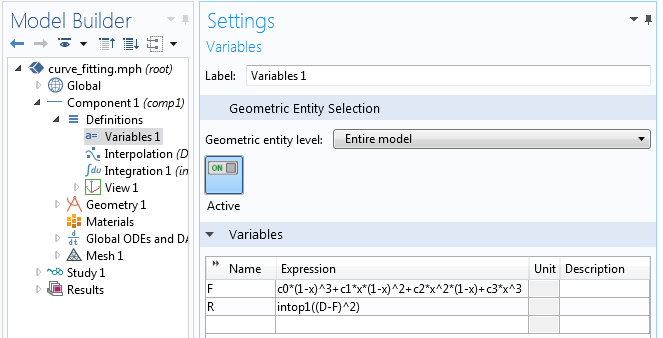
Визначення підбирається функції і цільової функції мінімізації.

Далі ми використовуємо інтерфейс Global Equations (Глобальні рівняння), щоб визначити чотири рівняння, яким задовольняють чотири наших коефіцієнта. Якщо ви пам'ятаєте, ми хочемо, щоб похідна функції R по кожному коефіцієнту зверталася в нуль. Використовуючи диференційний оператор d (f (x), x), ми можемо ввести цю умову так:

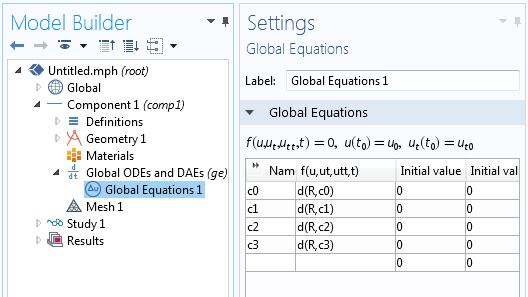
Глобальні рівняння використовуються для знаходження коефіцієнтів підбирається функції.

Нарешті, ми повинні накласти на нашу одновимірну область відповідну сітку. Як ви пам'ятаєте, раніше ми розмістили в кожній точці експериментальних даних геометричну точку. За допомогою підфункції Distribution (Розподіл) функції Edge Mesh (Сітка на ребрах) ми можемо розмістити рівно один елемент між кожною парою точок даних. Додаткових елементів не потрібно, так як ми припускаємо, що інтерполяція між точками набору даних лінійна, але і меншим числом елементів ми не обійдемося, не пропустивши деякі експериментальні точки даних.

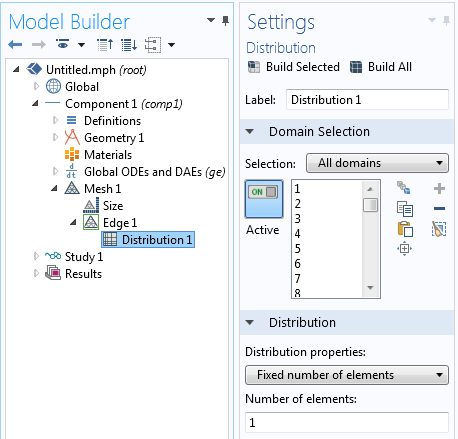
На кожному інтервалі даних повинен розташовуватися один елемент.

Тепер ми можемо вирішити стаціонарну задачу для знаходження чисельних значень коефіцієнтів, а потім побудувати результати. На графіку нижче ми бачимо побудований набір початкових точок, лінійну інтерполяцію між ними і підібрану функцію, отриману при розрахунку. Ми мінімізували інтеграл від квадрата різниці між цими кривими на даному інтервалі і отримали гладку і просту функцію, досить добре апроксимує наші дані.

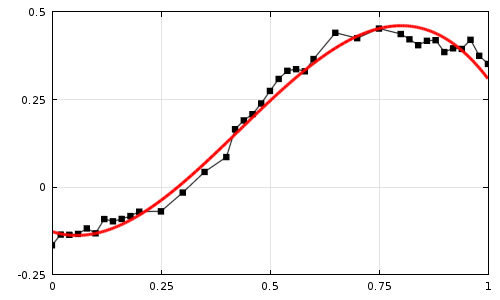
Експериментальні дані з лінійною інтерполяцією (чорний) і підібрана функція (червоний).

подальші розширення

Виконана нами робота насправді досить проста, і подібні криві можна розрахувати в будь-якому редакторі електронних таблиць і в багатьох інших програмних інструментах. Але цей же підхід дозволяє досягти набагато більшого. Ми не обмежені використанням даної підібраною функції. Ви можете вибрати будь-яку функцію, але краще вибирати функцію, яка є сумою набору ортогональних функцій. Наприклад, можна спробувати таку функцію:

F (x) = c_0 + c_1sin (\ pi x / 4) + c_2cos (\ pi x / 4) + c_3sin (\ pi x / 2) + c_4cos (\ pi x / 2)

Майте на увазі, що обчислюються коефіцієнти, що входять в підбраний функцію, повинні бути лінійними . Слід уникати нелінійних коефіцієнтів апроксимації, таких як F (x) = c_0 + c_1sin (\ pi x / c_3) + c_2cos (\ pi x / c_4), оскільки таке завдання може виявитися занадто нелінійної, щоб сходитися.

Але що робити, якщо у вас є двомірний або тривимірний набір даних? Ви можете застосувати до них точно такий же підхід. Різниця в тому, що тепер ми задаємо двомірну або тривимірну область. Області не обов'язково повинні бути декартовими, ви можете переключитися на іншу систему координат.

Давайте подивимося на деякий набір даних, виміряних на показаної нижче області.

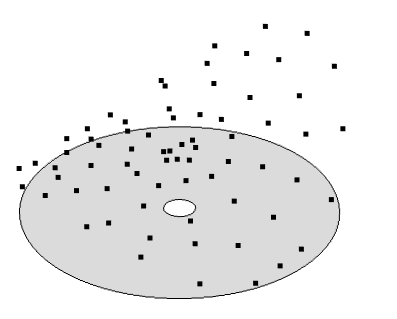
Набір даних на двомірної області. Ми хочемо підібрати поверхню, найбільш відповідну висот цих точок.

Так як дані зібрані на цій кільцеподібної області і, по видимості, змінюються в залежності від радіальної і азимутальной координат (r, \ theta), а не від декартових координат, ми можемо підібрати таку функцію:

F (x) = c_0 + c_1r cos (\ theta) + c_2 r sin (\ theta) + c_3 (2r ^ 2-1) + c_4 r ^ 2 cos (2 \ theta) + c_5 r ^ 2 sin (2 \ theta)

Ми можемо йти за такою ж процедурою, як і раніше. Тепер ми будемо інтегрувати по двомірної області, а не по кривій, і запишемо вираз з використанням циліндричної системи координат.

Розрахована поверхню найкращого наближення показана вище.

висновок

Ви бачите, що базові функціонально пакета COMSOL Multiphysics надають надзвичайно гнучкі можливості для пошуку кривих найкращого наближення в одновимірному, двомірному і тривимірному просторах за допомогою описаних методів.

У деяких випадках може знадобитися не обмежуватися простим підбором кривих і вводити додаткові обмеження. Тоді ви можете скористатися модулем Оптимізація , Який також може підбирати ці криві і вирішувати безліч інших завдань. Введення в підбір кривих за допомогою модуля Оптимізація і в пов'язану завдання оцінки параметрів ви знайдете тут: