Теорія без фактів може бути порожньою, але факти без теорії безглузді.
К.Боулдінг
Вступ
Часто доводиться чути, що ринки мінливі, що немає сталості. Це обумовлює неможливість прибутково торгувати на довгому проміжку часу. Чи так це? Давайте спробуємо підійти до цієї проблеми з наукової сторони. В якості методів дослідження виберемо економетричні . Чому саме ці? Ну, по-перше, тому що MQL спільнота любить точність, яку нам неупереджено забезпечать математика і статистика. А по-друге, якщо не помиляюся, про це ще не писали.
Відразу обмовлюся, що в рамках однієї статті поставлене завдання - чи можливо прибутково торгувати на довгому проміжку часу - не вирішити. Сьогодні я тільки опишу деякі методи діагностики для обраної моделі, які, сподіваюся, виявляться корисними для майбутнього дослідження.
Крім того, я постараюся, наскільки це можливо, викласти часом сухий матеріал, що включає в себе формули, теореми, гіпотези, доступним, що не пташиною мовою. Однак, я очікую, що читач буде знаком або ознайомиться з базовими статистичними поняттями, такими як: гіпотеза, статистична значимість, статистика (статистичний критерій), дисперсія, розподіл, вірогідність, регресія, автокорреляция і т.п.
1. Характеристики тимчасового ряду
Очевидно, що об'єкт аналізу - цінової ряд (його похідні), який є за своєю природою тимчасовим (Time series).
Економетристи вивчають тимчасової ряд з точки зору частотних методів (спектральний аналіз, вейвлетного аналіз) і методів тимчасової області (крос-кореляційний аналіз, автокореляційних аналіз). Читачеві раніше була представлена стаття "Будуємо аналізатор спектру", яка стосувалася частотних методів. Тепер я пропоную розглянути методи тимчасової області, зокрема, автокореляційна аналіз і аналіз умовної дисперсії.
Нелінійні моделі описують поведінку ц Енов часових рядів краще, ніж лінійні моделі. Тому в даній статті зосередимо свою увагу на вивченні нелінійних моделей.
Ціновим часових рядах притаманні специфічні особливості, врахувати які здатні лише певні економетричні моделі. До таких особливостям перш за все відносять: «товсті хвости», кластеризації волатильності і ефекти важеля.
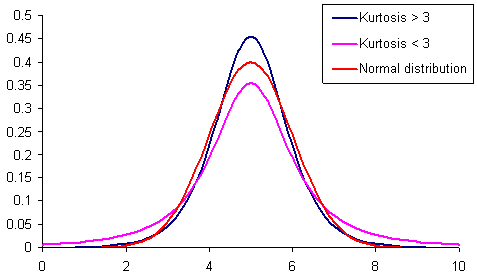
Малюнок 1. Розподілу з різним куртосісом.
На Рис.1 представлені 3 розподілу з різним куртосісом (гостровершинності). Розподіл, чия гостровершинності менше аналогічної нормального розподілу, найчастіше має «товсті хвости». Воно відображено рожевим кольором.
Розподіл нам потрібно для того, щоб відобразити щільність ймовірності випадкової величини, якої ми вважаємо значення досліджуваного ряду.
Під кластеризацией (від англ. Cluster - пучок, скупчення, концентрація) волатильності розуміється наступне. За проміжком часу з високою волатильністю слід такий же, а за проміжком з низькою - ідентичний. Якщо вчора ціни сильно коливалися, то і сьогодні, найімовірніше, вони будуть коливатися так само сильно. У цьому сенсі, присутня деяка інерція волатильності. На Рис.2 показано, що волатильність має пучкообразную форму.

Малюнок 2. Волатильність денних доходностей пари usdjpy, її кластеризація.
Ефект важеля полягає в тому, що на падаючому ринку волатильність вище, ніж на зростаючому. Виходить так тому, що при зниженні цін акцій збільшується коефіцієнт важеля, що залежить від ставлення позикового і власного капіталу. Але швидше за це явище стосується фондового ринку, а не валютного. Далі цей ефект розглядатися не буде.
2. GARCH-модель
Отже, наша основна мета - зробити прогноз валютного курсу (ціни) за допомогою деякої моделі. Економетристи використовують математичні моделі, описуючи ті чи інші явища, піддаються кількісній оцінці. Якщо говорити простіше, то вони підводять під явище якусь формулу. І таким чином описують це явище.
З огляду на те, що досліджуваний часовий ряд має властивості, зазначені вище, оптимальною моделлю, яка враховує ці властивості, можна назвати нелінійну модель. Одна з найбільш універсальних нелінійних моделей - це GARCH-модель . Чим вона нам допоможе? Вона буде враховувати в своєму тілі (формулою) волатильність ряду, тобто мінливість дисперсії на різних інтервалах спостереження. Економетристи називають це явище мудрованим словом гетероскедастичності (від грец. Hetero - різний, skedasis - дисперсія).
Якщо ми безпосередньо подивимося на формулу, то побачимо, що дана модель передбачає, що на поточну мінливість дисперсії (σ2 t) впливають як попередні зміни показників (ε 2 t -i), так і попередні оцінки дисперсії (т.зв. «старі новини ») (σ2 t -i):
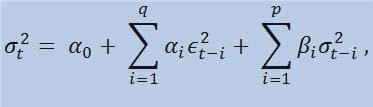
з обмеженнями
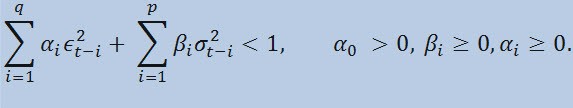
Де, ε t - ненормовані інновації; α 0, β i, α i, q (порядок ARCH-членів ε 2), p (порядок GARCH-членів σ2) - оцінювані параметри і порядок моделей.
3. Індикатор доходностей
Насправді оцінювати ми будемо не сам цінової ряд, а ряд доходностей. Логарифм зміни ціни (безперервно нараховується прибутковість) визначається як натуральний логарифм процентної прибутковості, а саме:
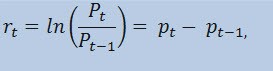
де,
- P t - це значення цінового тимчасового ряду в момент часу t;
- P t-1 - це значення цінового тимчасового ряду в момент часу t-1;
- pt = ln (P t) - це натуральний логарифм Pt.
На практиці, основна причина, по якій робота з прибутковістю активів є більш кращою, ніж з безпосередніми цінами активів, полягає в тому, що прибутковості мають більш привабливі статистичні властивості.
Отже, давайте створимо для початку індикатор доходностей ReturnsIndicator.mq5, який в подальшому нам дуже знадобиться. Тут я дозволю собі послатися на статтю «Призначені для користувача індикатори в MQL5 для початківців» , В якій доступно викладений алгоритм створення індикатора. Тому наведу тільки програмний код, безпосередньо реалізує вказану формулу. Думаю, що він дуже простий, і пояснювати нічого не потрібно.
int OnCalculate (const int rates_total, const int prev_calculated, const int begin, const double & price []) {int start; if (prev_calculated <2) start = 1; else start = prev_calculated- 1; for (int i = start; i <rates_total; i ++) {ReturnsBuffer [i] = MathLog (price [i] / price [i- 1]); } Return (rates_total); } Єдине, що хотілося б відзначити, по своїй суті ряд доходностей завжди менше вихідного ряду на 1 елемент. Тому масив доходностей ми будемо розраховувати з другого елементу, а перший завжди буде дорівнює 0.
Отже, за допомогою індикатора ReturnsIndicator ми отримали той похідний тимчасової ряд, який стане об'єктом наших досліджень.
4. Статистичні тести
Тепер настає очер їдь статистичних тестів. Вони проводяться для того, щоб визначити, чи є в тимчасовому ряді якісь ознаки, що підтверджують доцільність застосування тієї чи іншої моделі. У нашому випадку т акой моделлю стане GARCH-модель.
За допомогою Q-тесту Льюнг-Боксу-Пірса перевіримо, чи випадкові автокорреляцііряда або є якась залежність. Для цього нам доведеться написати нову функцію. Тут під автокореляцією ми розуміємо кореляцію (вірогідну зв'язок) між значеннями одного і того ж часового ряду X (t) в моменти часу t1 і t2. Якщо моменти часу t1 і t2 є сусідніми (тобто слідують один за одним), то ми шукаємо зв'язок членів ряду і пересунути на одну одиницю часу членів того ж ряду: x1, x2, x3, ... і x1 + 1, x2 + 1, x3 + 1, ... Таке запізнювання пересунути членів називається лагом (від англ. lag - відставання, затримка, запізнювання). Значення лага може бути будь-яким позитивним цілим числом.
Тут я зроблю невеликий ліричний відступ і скажу ось про що. Наскільки я знаю, ні в мові С ++, ні в MQL5 немає стандартних бібліотек, що охоплюють складні і не дуже статистичні розрахунки. Зазвичай такі розрахунки проводяться в спеціальних статистичних пакетах. Особисто для мене набагато простіше було б скористатися такими пакетами, як наприклад Matlab, STATISTICA 9 і подібними, щоб вирішити поставлене завдання. Але я вирішив відмовитися від використання зовнішніх бібліотек, з одного боку, щоб продемонструвати, наскільки сама мова MQL5 являє собою потужний інструмент для розрахунків, а з іншого ... я сам в процесі написання MQL коду багато чому навчився.
Тепер потрібно зауважити наступне. Для проведення Q-тесту будуть потрібні комплексні числа. Тому я створив клас Complex. В ідеалі він звичайно повинен називатися CComplex. Але я трохи дозволив собі розслабитися. Упевнений, що читач є підготовленим, і йому не потрібно пояснювати, що собою являє комплексне число . Особисто мені не дуже сподобалися функції, які розраховують перетворення Фур'є, які з'являлися і на сайті MQL5, і на сайті MQL4, де неявно фігурували комплексні числа. Тим більше, що ще одна перешкода мало місце - це неможливість, зокрема, перевантажувати в MQL5 арифметичні оператори. Довелося шукати інші підходи і обходити стандартну сішную нотацію. Клас комплексних чисел я представив приблизно так:
class Complex {public: double re, im; // re -вещественная частина комплексного числа, im - уявна public: void Complex () {}; void setComplex (double rE, double iM) {re = rE; im = iM;}; // set-метод (1-й варіант) void setComplex (double rE) {re = rE; im = 0;}; // set-метод (2-й варіант) void ~ Complex () {}; void opEqual (const Complex & y) {re = y.re; im = y.im;}; void opPlus (const Complex & x, const Complex & y); // void opPlusEq (const Complex & y); // void opMinus (const Complex & x, const Complex & y); // void opMult (const Complex & x, const Complex & y); // * void opMultEq (const Complex & y); // * = (1-й варіант) void opMultEq (const double y); // * = (2-й варіант) void conjugate (const Complex & y); // сполучення комплексних чисел double norm (); // нормалізація}; Тобто, наприклад, операцію складання двох комплексних чисел тепер можна провести за допомогою методу opPlus, віднімання - opMinus і т.д. Якщо просто в коді написати c = a + b (де a, b, с - це комплексні числа), то компілятор збунтується. Але прийме такий вислів: c.opPlus (a, b).
Користувач за необхідності може розширити набір методів класу Complex. Наприклад, можна додати оператор ділення.
Ще мені знадобилися допоміжні функції, що обробляють масиви комплексних чисел. Тому я їх вивів за рамки класу Complex, щоб не зацикливать обробку елементів масиву класу Complex, а працювати з переданими по посиланню масивами безпосередньо. Всього таких функцій три:
- getComplexArr (повертає двовимірний масив дійсних чисел з масиву комплексних);
- setComplexArr (повертає масив комплексних чисел з одновимірного масиву дійсних чисел);
- setComplexArr2 (повертає масив комплексних чисел з двовимірного масиву дійсних чисел).
Потрібно зауважити, що ці функції повертають масиви, передані їм за посиланням. Тому в їх тілі відсутній оператор return. Але розмірковуючи логічно, по-моєму, можна говорити про повернення, незважаючи на тип void.
Клас комплексних чисел і допоміжних функцій визначено в заголовки Complex_class.mqh.
Потім нам знадобляться при проведенні тесту автокореляційна функція і функції перетворення Фур'є . І тут виникає необхідність у створенні нового класу, який я назву CFFT. Він буде обробляти масиви комплексних чисел для Фур'є-перетворень. Фур'є-клас я представив приблизно так:
class CFFT {public: Complex Input []; Complex Output []; public: bool Forward (const uint N); bool InverseT (const uint N, const bool Scale = true); bool InverseF (const uint N, const bool Scale = false); void setCFFT (Complex & data1 [], Complex & data2 [], const uint N); set-метод (1-й варіант) void setCFFT (Complex & data1 [], Complex & data2 []); set-метод (2-й варіант) protected: void Rearrange (const uint N); void Perform (const uint N, const bool Inverse); void Scale (const uint N); };Потрібно відзначити, що всі Фур'є-перетворення проводяться з масивами, довжина яких задовольняє умові 2 ^ N (де N - це ступінь двійки). Як правило, довжина масиву не дорівнює 2 ^ N. Тоді довжина масиву збільшується до такого значення 2 ^ N, що 2 ^ N> = n, де n - це довжина масиву. Додані елементи масиву дорівнюють нулю. Така обробка масиву відбувається в тілі функції autocorr за допомогою службової функції nextpow2 і функції pow:
int nFFT = pow (2, nextpow2 (ArraySize (res)) + 1);Так, якщо ми маємо вихідний масив, довжина (n) якого дорівнює 73585, то функція nextpow2 поверне нам значення 17, де 2 ^ 17 = 131072. Тобто яке значення більше n на pow (2, ceil (log (n) / log (2))). Потім ми обчислимо значення nFFT: 2 ^ (17 + 1) = 262144. Це буде довжина службового масиву, елементи якого з 73585-го по 262143-ий дорівнюватимуть нулю.
Фур'є-клас визначений в заголовки FFT_class.mqh.
Знову в цілях економії пропущу опис реалізацій класу CFFT. Ті, хто цікавиться зможуть самі перевірити їх в доданому включається файлі. Давайте перейдемо тепер безпосередньо до автокореляційної функції.
Отже, ми вирахували значення АКФ для заданої кількості лагів. Тепер можна використовувати автокорреляционную функцію для Q-тесту. Сама функція тесту буде виглядати приблизно так:
void lbqtest (bool & H [], double & rets []) {double lags [3] = {10.0, 15.0, 20.0}; int maxLags = 20; double ACF []; ArrayResize (ACF, 21); double acf []; ArrayResize (acf, 20); autocorr (ACF, rets, maxLags); for (int i = 0; i <20; i ++) acf [i] = ACF [i + 1]; double alpha [3] = {0.05, 0.05, 0.05}; double idx []; ArrayResize (idx, maxLags); int len = ArraySize (rets); int arrLags []; ArrayResize (arrLags, maxLags); double stat []; ArrayResize (stat, maxLags); double sum []; ArrayResize (sum, maxLags); double iACF []; ArrayResize (iACF, maxLags); for (int i = 0; i <maxLags; i ++) {arrLags [i] = i + 1; idx [i] = len-arrLags [i]; iACF [i] = pow (acf [i], 2) / idx [i]; } Cumsum (sum, iACF); for (int i = 0; i <maxLags; i ++) stat [i] = sum [i] * len * (len + 2); double stat1 []; ArrayResize (stat1, ArraySize (lags)); for (int i = 0; i <ArraySize (lags); i ++) stat1 [i] = stat [lags [i] - 1]; double pValue [ArraySize (lags)]; for (int i = 0; i <ArraySize (lags); i ++) {pValue [i] = 1-gammp (lags [i] / 2, stat1 [i] / 2); H [i] = alpha [i]> = pValue [i]; }} Отже, наша функція проводить Q-тест Льюнг-Боксу-Пірса і повертає масив логічних значень для заданих лагов. Тут потрібно уточнити, що тест Льюінга-Боксу є так званим portmanteau тестом (приблизний переклад з англ. - об'єднаний тест). Це означає, що перевіряється деяка група лагов на наявність автокореляції аж до зазначеного лага. Зазвичай перевіряють чи є автокорреляция до 10-го, 15-го і 20-го лага включно. Висновок про наявність автокореляції в усьому ряді робиться за останнім значенням елемента масиву H, тобто від першого лага до двадцятого.
Якщо елемент масиву дорівнює false, то нульова гіпотеза про те, що на попередніх і заданому лагу не має місце автокорреляция, не відкидається. Тобто при значенні false автокорреляции немає. В іншому випадку, тест вказує на наявність автокореляції. Тому приймається альтернативна нульовий гіпотеза про наявність автокореляції при значенні true.
Трапляється так, що автокореляції в ряді доходностей не виявляється. Тоді для більшої переконливості тестують квадрати доходностей. Висновок про прийняття або відкиданні нульової гіпотези робиться так само, як і при тесті вихідного ряду доходностей. Навіщо беруться квадрати доходностей? - Таким чином ми штучно збільшуємо можливу невипадково автокорреляционную складову досліджуваного ряду, яку потім і виявляємо в рамках початкових значень довірчих меж. Теоретично можна брати і куби, і інші міри доходностей. Але це вже зайва статистичне навантаження, при якій втрачається сенс у тестуванні.
Можна помітити, що в кінці тіла функції Q-тесту при розрахунку р-значення (читається як пі-значення) з'явилася ще одна функція gammp (x1 / 2, x2 / 2). Вона дозволяє обчислити неповну гамма-функцію для відповідних елементів. Взагалі-то нам була потрібна спочатку кумулятивна функція χ2-розподілу (Читається як хі-квадрат-розподілу). Але саме вона є окремим випадком гамма розподілу .
Загалом, для підтвердження того, що слід скористатися GARCH-моделлю, достатньо отримати позитивне значення будь-якого з лагов Q-тесту. Крім того, Економетристи проводять ще такий тест, як ARCH-тест Енгл, перевіряючий наявність умовної гетероскедастичності. Але, гадаю, що нам цілком достатньо Q-тесту для початку. Він є самим універсальним.
Тепер, коли у нас є всі необхідні функції для проведення зазначеного тесту, потрібно подумати про те, як вивести отримані результати на екран. Для цього я написав ще одну функцію lbqtestInfo, яка і виведе нас результати економетричного тестування у формі вікна повідомлень, а діаграми автокореляцій - прямо на графік досліджуваного інструменту.
Давайте подивимося, що у нас вийшло на конкретному прикладі. Першим інструментом для дослідження я вибрав пару usdjpy. Спочатку я відкрив графік пари у вигляді ламаної лінії (за цінами закриття) і завантажив призначений для користувача індикатор ReturnsIndicator для ілюстрації ряду доходностей. Графік максимально стиснув, щоб краще бачити кластеризацию волатильності індикатора. Потім запустив на виконання скрипт GarchTest. Можливо, що у нас з Вами різні дозволи моніторів, тому скрипт запитає Вас, якого розміру діаграми в пікселях Ви бажаєте отримати. Мій стандарт 700 * 250.
Кілька прикладів тестування наведено на Рис.3.
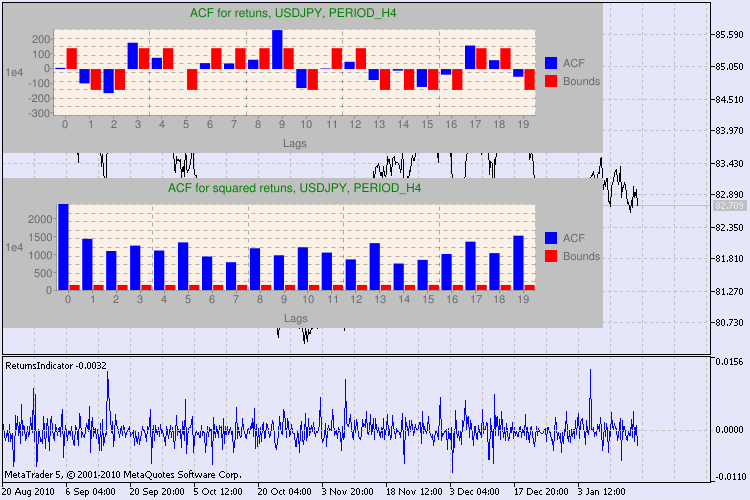
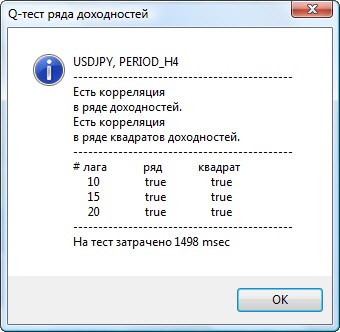
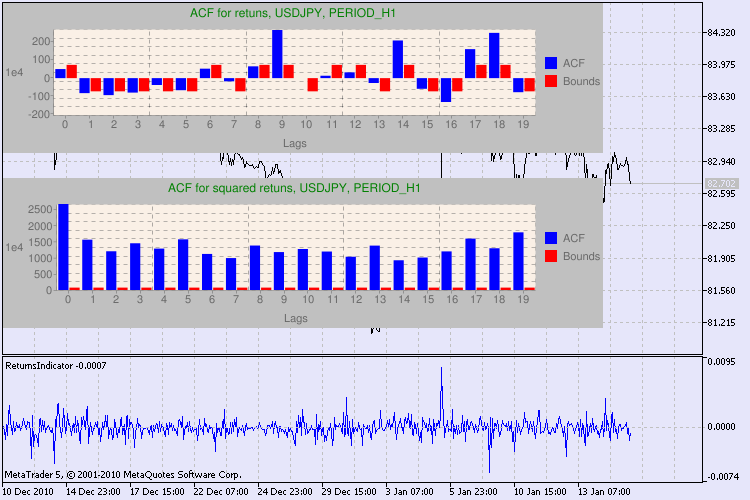
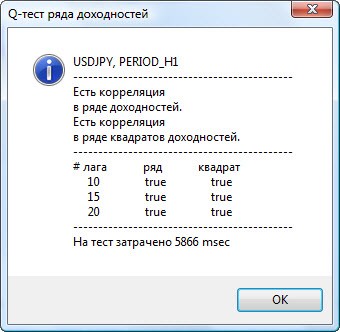
Малюнок 3. Результати Q-тесту і діаграми автокореляцій для пари usdjpy для різних тайм-фреймів.
Так, я довго шукав варіант відображення діаграми на графіку інструменту в MetaTrader 5. І найоптимальнішим вважав - скористатися бібліотекою для побудови діаграм засобами Google Chart API, про яку розказано в однойменній статті .
Як інтерпретувати виведену інформацію? Давайте розберемося. Вгорі вікна графіка знаходиться діаграма usdjpy доходностей. Діаграма нижче - це діаграма квадратів доходностей для зазначеної пари. Там взагалі все ясно - повна перемога синіх стовпців. Діаграми для годинного тайм-фрейму аналізуються аналогічно.
Пару слів про опис осей діаграми. З віссю x все ясно - на ній представлені індекси лагов. На осі y вказано експоненціальне значення, на яке було помножено початкове значення АКФ. Так, 1e4 означає, що вихідне значення помножено на 1e4 (1e4 = 10000), а 1e2 - на 100 і т.д. Таке множення було зроблено для читабельності діаграми.
Вгорі діалогового вікна відображено назву пари або кросу і тайм-фрейм інструменту. Потім йдуть 2 пропозиції, які вказують на наявність або відсутність автокорреляция в вихідному ряді доходностей і в ряді квадратів доходностей. Потім перераховано 10-ий, 15-ий і 20-ий лаг, значення автокореляції в вихідному ряді і в ряді квадратів. Тут для автокореляції вказано відносне значення у вигляді булевого прапора при Q-тесті: чи є автокорреляция на попередніх і заданому лагу.
У підсумку, якщо ми бачимо, що автокорреляция на попередніх і заданому лагу присутній, то прапор буде дорівнює true, інакше - false. У першому випадку наш ряд є "клієнтом" для застосування нелінійної GARCH-моделі, а в другому - потрібно використовувати більш прості аналітичні моделі. Уважний читач легко помітить, що вихідні ряди доходностей пари usdjpy незначно корелюють самі з собою, особливо старшого тайм-фрейму. Але ряди квадратів доходностей вже проявляють автокореляцію.
Внизу вікна вказано час в мсек, витрачений на тестування.
Все тестування ми проводили за допомогою скрипта GarchTest.mq5.
Висновки
У своїй статті я описав те, як Економетристи досліджують тимчасові ряди, а точніше з чого вони починають свої дослідження. При цьому довелося самому кодувати багато функцій і деякі типи даних (наприклад комплексні числа). Можливо, що візуальна оцінка вихідного ряду дає приблизно схожий результат, що і оцінка економетрична. Однак, ми домовилися, що при вивченні проблеми будуть використовуватися точні методи. Так, досвідчений лікар може поставити діагноз хворого без застосування складної техніки і методології. Але, як правило, він вивчає недуга хворого ретельно і скрупульозно.
Що нам дає описаний в статті підхід? Застосування нелінійної GARCH-моделі дозволяє, по-перше, формально представити досліджуваний ряд з математичної точки зору, а по-друге, створити прогноз на задану кількість кроків. Що допоможе нам надалі симулювати поведінку ряду в прогнозної області і протестувати будь-який з торгових експертів на підставі прогнозованих даних.
Розташування файлів:
#File
Path
1
ReturnsIndicator.mq5% MetaTrader% \ MQL5 \ Indicators 2
Complex_class.mqh% MetaTrader% \ MQL5 \ Include 3
FFT_class.mqh% MetaTrader% \ MQL5 \ Include 4
GarchTest.mq5% MetaTrader% \ MQL5 \ Scripts
Файли і опис бібліотеки google_charts.mqh і Libraries.rar можна скачати в зазначеній раніше статті .
Використовувана література:
- Analysis of Financial Time Series, Ruey S. Tsay, 2nd Edition, 2005. - 638 pp.
- Applied Econometric Time Series, Walter Enders, John Wiley & Sons, 2nd Edition, 1994. - 448 pp.
- Bollerslev, T., RF Engle, and DB Nelson. "ARCH Models." Handbook of Econometrics. Vol. 4, Chapter 49, Amsterdam: Elsevier Science BV
- Box, GEP, GM Jenkins, and GC Reinsel. Time Series Analysis: Forecasting and Control. 3rd ed. Upper Saddle River, NJ: Prentice-Hall, 1994.
- Numerical Recipes in C, The Art of Scientific Computing, 2nd Edition, WH Press, BP Flannery, SA Teukolsky, WT Vetterling, 1993. - 1020 pp.
- Голуб Дж., Ван Лоун Ч. Матричні обчислення: Пер. з англ. - М .: Світ, 1999. - 548 с., Іл.
- Поршнев С.В. "Обчислювальна математика. Курс лекцій" C- Пб.: БХВ-Петербург, 2004. - 314 с.
Чи так це?
Чому саме ці?
Чим вона нам допоможе?
Навіщо беруться квадрати доходностей?
Як інтерпретувати виведену інформацію?
Що нам дає описаний в статті підхід?
